Victor Landeau

Passionné par le développement de solutions à base de Machine Learning, de l'analyse du problème à l'utilisation en production

Retour sur l'importance de la mesure de distance

K-Means, clustering hiérarchique, DBSCAN, OPTICS, modèle de mélange gaussien… Le moins qu’on puisse dire, c’est que les algorithmes de clustering existants sont nombreux et se basent sur des techniques très différentes les unes des autres. Les data scientists peuvent ainsi passer un certain temps à les essayer tous, en faisant à chaque fois varier leurs hyperparamètres. Mais d’un autre côté, le choix de la mesure de distance associée au processus de clustering est bien souvent négligée, alors même qu’elle a un effet prépondérant sur le résultat final.

Nous allons analyser en quoi la bonne détermination de cette mesure de distance est essentielle pour obtenir un clustering utile. Nous verrons ensuite une manière d’obtenir une telle mesure à la suite d’une modélisation supervisée, notamment grâce à une forêt d’arbres aléatoires, méthode inspirée des travaux originaux de Leo Breiman et Adele Cutler.

La distance, une notion à la base de l’évaluation de la qualité du clustering

Le clustering est, rappelons-le, une problématique typique du champ de l’apprentissage non supervisé. Et, en tant que tel, la qualité de ses résultats est par essence difficile à évaluer. En effet, le but d’un algorithme non-supervisé est d’extraire des informations, des patterns jusqu’alors inconnus à partir d’un ensemble de données. Il n’est donc a priori pas possible de comparer les prédictions de notre modèle avec une source de vérité indiscutable, comme ce qui se fait dans l’apprentissage supervisé.

Dans le cas particulier du clustering, notre but est d’extraire des regroupements d’échantillons, de sorte que les échantillons au sein d’un même cluster soient les plus homogènes possibles, et les plus différents possibles des échantillons en dehors dudit cluster¹. Quand on parle d’homogénéité et de différence, cela renvoie ici au calcul d’une mesure de distance entre les échantillons deux à deux. La mesure de distance est donc à la base de l’évaluation de la qualité de notre clustering, et tient un rôle très similaire à celui de la fonction de coût dans un problème d’apprentissage supervisé. Tout comme la fonction de coût, sa détermination doit essentiellement se baser sur la compréhension du problème que l’on cherche à résoudre.

Application à une problématique de fidélisation des clients

Pour mieux comprendre, prenons une problématique business typique à laquelle peut participer un data scientist : la réduction du taux d’attrition, ou churn. Beaucoup d’entreprises, et notamment celles de télécommunication, ont à coeur dans leur business model de fidéliser leurs clients, et d’éviter que ceux-ci résilient leur abonnement et s’en aillent signer chez un concurrent. Pour cela, il est très important pour elles d’être capable de détecter les clients ayant une forte probabilité de “churner”, pour ensuite pouvoir s’adresser à eux avec un message approprié, et tenter ainsi de les conserver dans leur clientèle.

La première partie de cet objectif est généralement interprétée comme une problématique d’apprentissage supervisé : on cherche à prédire pour chaque client sa probabilité de résilier son abonnement, en apprenant de ceux qui l’ont effectivement résilié par le passé. La deuxième partie, par contre, est plus sujette à interprétation : comment peut-on décider de la façon de construire les campagnes marketing de fidélisation ? Ne s’agit-il pas purement d’une problématique purement métier ?

Alors oui, bien évidemment, l’expertise métier est ici essentielle pour déterminer ne serait-ce que la manière de s’adresser au client, et le message que l’on va lui donner. Mais cela ne veut pas dire que la Data Science ne peut pas faciliter et accélérer cette procédure, notamment en permettant de déterminer des regroupements intelligents de clients à fort potentiel de churn, afin de pouvoir adresser rapidement les clients similaires avec un message adapté.

C’est à cette problématique que nous allons nous atteler dans le reste de l’article, en se basant sur les données de Telco, un opérateur de télécommunication. Pour pouvoir mieux appréhender les expérimentations qui seront décrites, vous pourrez vous référer au notebook contenu sur ce projet github.

L’utilisation du modèle supervisé pour déterminer la mesure de distance

La méthode la plus classique pour déterminer la distance entre chacun des échantillons consiste à :

• prendre toutes les variables explicatives (ou features) à disposition, qui auraient un rapport de prêt ou de loin avec le problème que l’on cherche à résoudre ;
• centrer réduire chacune d’entre elles ;
• appliquer une distance euclidienne.

De cette manière, on peut s’assurer qu’aucune des features ne prenne d’importance disproportionnée dans le clustering, du simple fait que sa variance serait beaucoup plus importante que celles des autres features (pour une question d’échelle, généralement). Ici, toutes les features auront la même importance dans le clustering.

Mais en faisant ainsi, on ne prend pas en compte l’importance relative des différentes features dans notre problématique : même si l’on pense que toutes peuvent avoir un lien avec les raisons pour lesquelles l’abonné pourrait souhaiter changer d’opérateur, certaines sont certainement plus prépondérantes que d’autres, ou en tout cas seraient plus importantes que les autres dans le choix du message à adresser à ces clients.

En cas de difficulté à récupérer ce type d’information auprès des experts métiers, une manière de faire est de l’extraire de l’outil qui nous a permis en premier lieu de déterminer que le client considéré était à risque de churn : le modèle supervisé. Que cela soit en utilisant des techniques spécifiques à l’algorithme utilisé, tel que le fait de récupérer la valeur des poids affectés aux différentes variables d’un régression linéaire, ou la probabilité pour chaque variable d’être la cause d’un embranchement (split) au sein d’un arbre de décision, ou en utilisant des méthodes plus générales telles que LIME ou les valeurs de shapley, il est aujourd’hui possible de déterminer l’importance relative des différentes variables explicatives pour la plupart des modèles de machine learning supervisés.

On peut alors calculer une nouvelle mesure de distance entre les points en suivant les étapes suivantes :

• Prendre toutes les variables explicatives utilisées pour notre modèle supervisé ;
• Les centrer réduire, afin qu’elles aient toutes la même variance ;
• Les multiplier chacune par un poids correspondant à leur importance au sein du modèle supervisé, afin que leur variance devienne proportionnelle à cette mesure d’importance ;
• Appliquer une mesure de distance classique telle que la distance euclidienne.

Un algorithme particulier pour le cas des forêts d’arbres aléatoires

Dans le cas d’une forêt d’arbres aléatoires, il est possible d’extraire directement une mesure de distance entre les différents échantillons du fonctionnement même de l’algorithme, comme la montré Leo Breiman dans son travail originel. Quand on y réfléchit, l’application d’une forêt d’arbre aléatoire en elle-même permet déjà de segmenter les données : chaque arbre rangeant chaque échantillon dans une feuille spécifique, on obtient de fait une segmentation complète et assez fine de l’espace.

Voire beaucoup trop fine, même : la probabilité que deux échantillons se retrouvent dans la même feuille sur l’ensemble des arbres de la forêt est, du fait du principe même du bagging, très très faible. Si l’on veut avoir un nombre de clusters significativement supérieur au nombre d’échantillons, il va falloir trouver une autre manière de regrouper les échantillons. Pour cela, on va plutôt interpréter le fait que deux échantillons se retrouvent dans la même feuille sur un arbre donné comme un indicateur de la similarité de ces échantillons.

Ainsi, une mesure possible est de considérer que la distance entre deux échantillons correspond à la proportion d’arbres pour lesquels ces deux échantillons se retrouvent sur une feuille différente. Cela est assez facilement applicable en python, en utilisant la fonction apply d’une instance entrainée de la classe RandomForestClassifier, puis en utilisant l’encodage ainsi généré pour calculer la distance entre chacun des points deux à deux, en utilisant la distance de Hamming :

encoding = rf.apply(x)
distance_matrix = sklearn.metrics.pairwise_distances(encoding, metric="hamming")

On pourra ensuite utiliser la matrice de distance ainsi obtenue pour établir le clustering en lui-même, en utilisant par exemple un algorithme de clustering hiérarchique :

aggl_clustering_from_rf = AgglomerativeClustering(n_clusters=n_clusters, 
                                                  affinity="precomputed", 
                                                  linkage="average")
aggl_clustering_from_rf.fit(distance_matrix)

Quel est l’impact de ces différentes méthodologies

Comme on peut le voir dans le notebook, l’utilisation de ces différentes mesures de distance sur notre problématique de churn donne des clustering très différents, même si on utilise au final le même algorithme de clustering avec les même hyperparamètres. Analysons donc la distribution au sein des différents clustering testés de trois des variables explicatives les plus importantes dans le modèle de détermination de la propension à churner :

• Le montant payé chaque mois (MonthlyCharges) ;
• L’ancienneté du client au sein de Telco (tenure) ;
• Le mode de paiement (PaymentMethod).

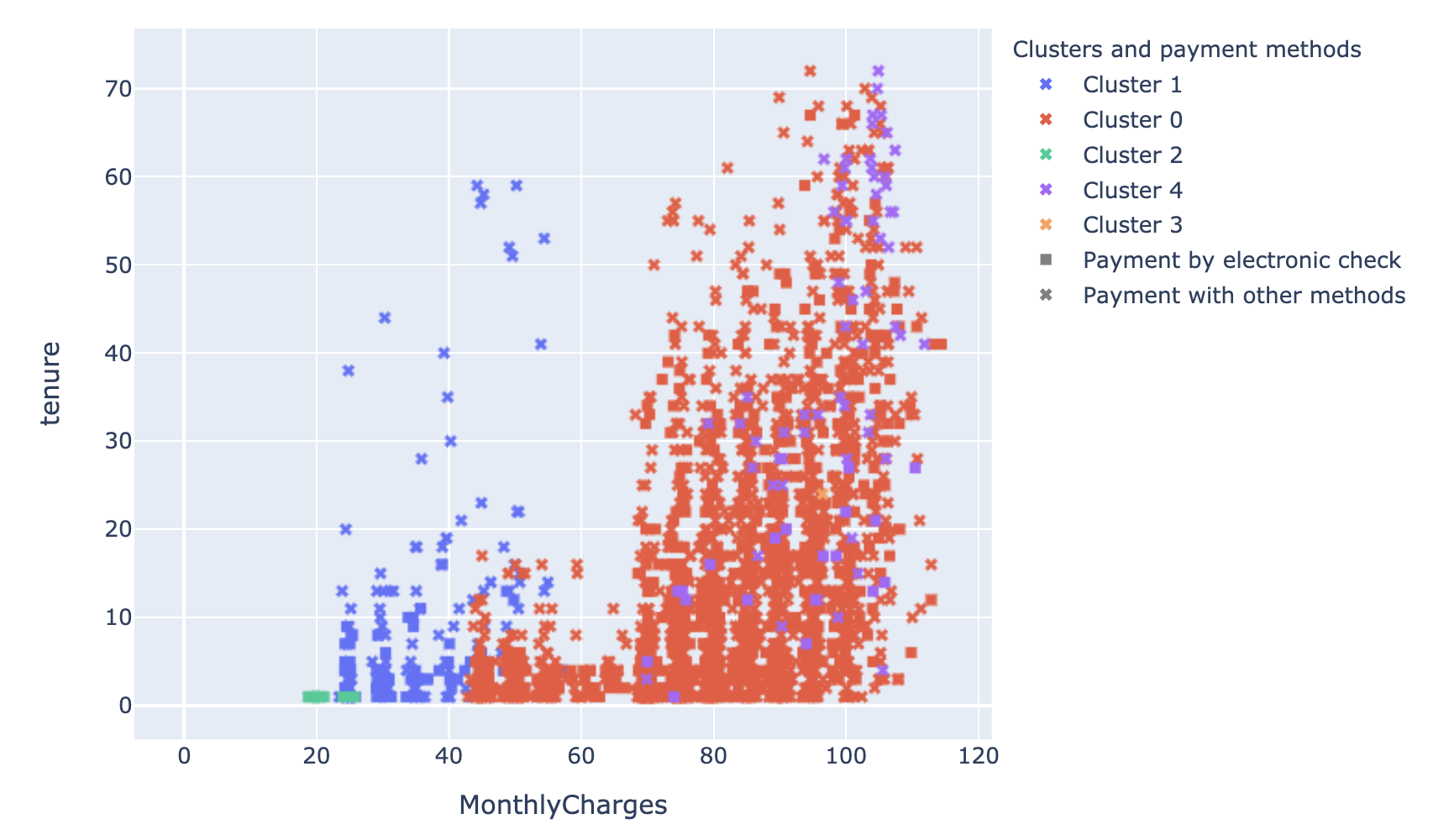
Lorsqu’on regarde les clusters résultant de la première mesure de distance décrite (distance euclidienne où toutes les variables ont le même poids), on se rend compte qu’il n’est pas vraiment possible d’interpréter le clustering en fonction de ces quelques variables business essentielles, parce qu’il donne aussi beaucoup d’importance à toutes les autres variables. Cela n’est pas un problème en soi, mais on peut s’interroger sur la pertinence de ces autres variables étant donné qu’elles ont un poids beaucoup moins important dans la détermination de la probabilité du client à churner.

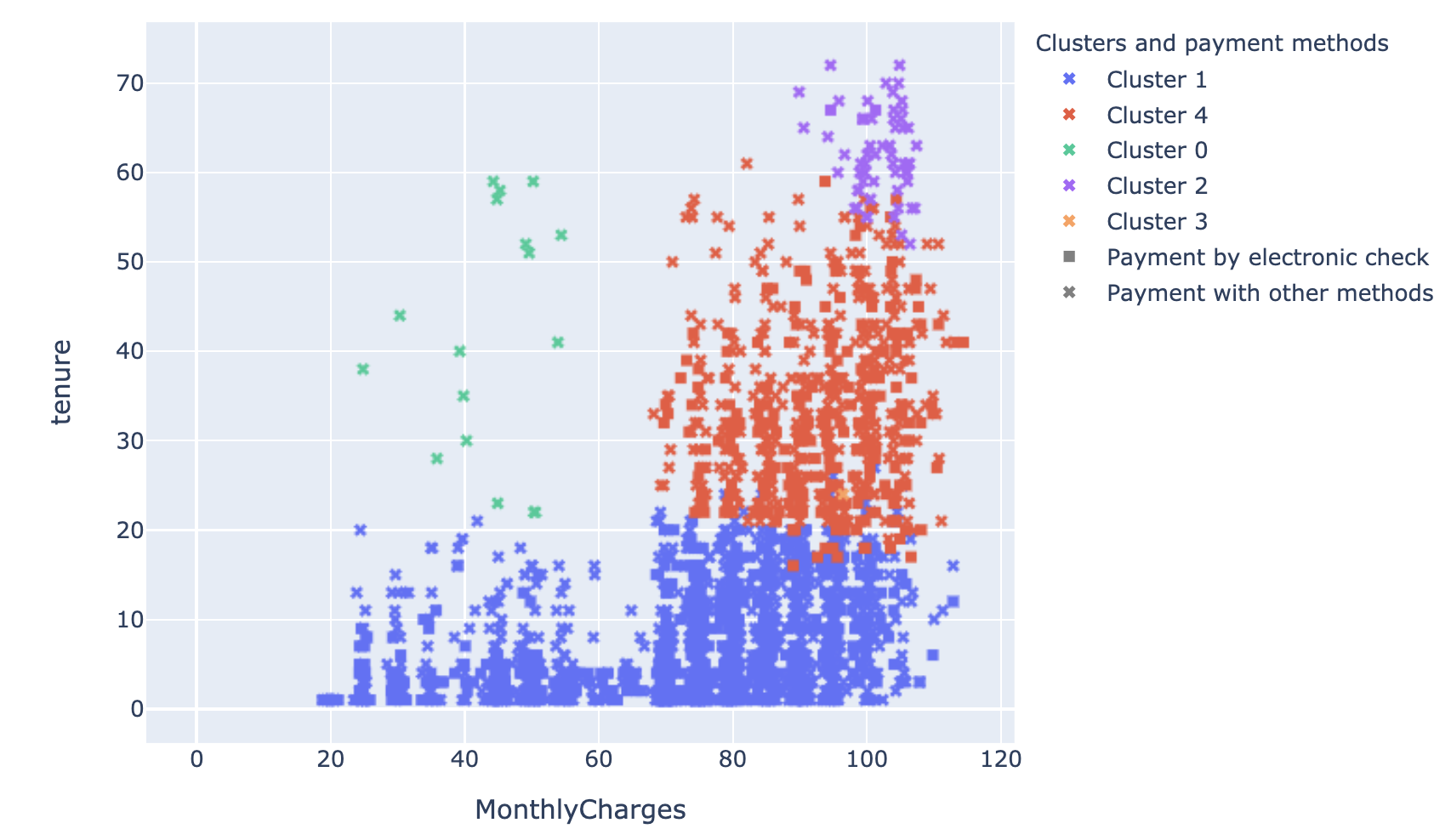
Lorsqu’on prend en compte l’importance relative des variables dans la potentialité de churn pour effectuer le clustering, on obtient un résultat qu’on peut visualiser bien plus facilement. En effet, le modèle semble s’être focalisé sur le montant payé et l’ancienneté de l’abonnement pour effectuer le partitionnement.

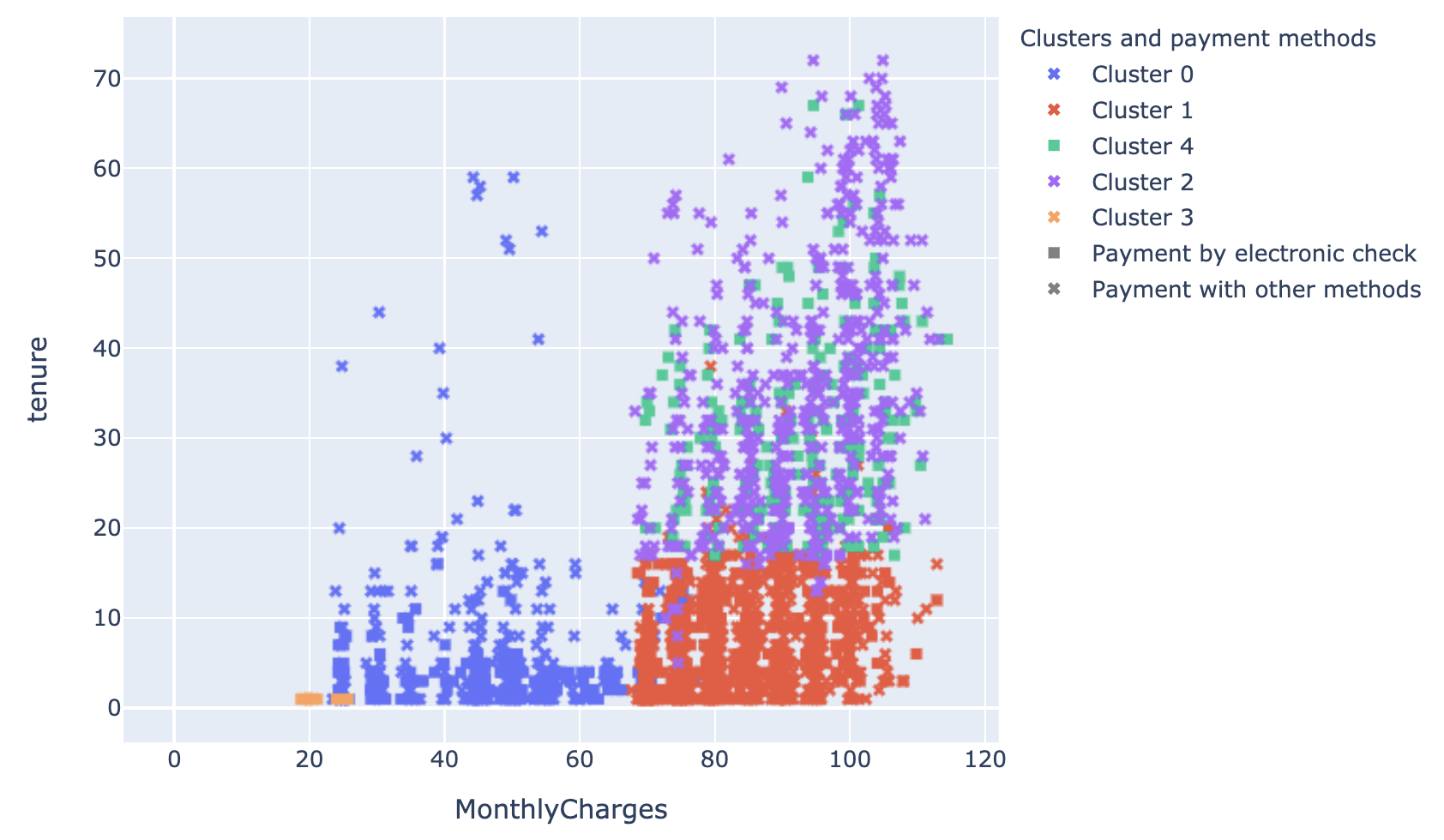
Enfin, lorsqu’on utilise la méthode décrite dans le paragraphe précédent, on obtient un résultat assez similaire à ce qu’on a eu juste avant, à une différence près : il semblerait que, pour notre forêt d’arbres aléatoires, l’accroissement de l’ancienneté ne change plus grand chose à la propension à churner au bout d’un certain niveau. Le mode de paiement peut alors être une information bien plus intéressante. C’est en tout cas ce que semble indiquer la distinction entre le cluster 2 et le cluster 4. Le cluster 2 implique ainsi quasi exclusivement des paiements par chèque électronique, tandis que le 4 regroupant l’ensemble des autres méthodes de paiement.

Avantages et inconvénients de la méthode proposée

La méthode proposée nous a permis de prendre en compte dans le clustering des informations complexes telle que le changement d’importance relative des différentes variables en fonction du niveau de chacune d’entre elle. Cela nous permet de créer un clustering qui s’ancre encore plus dans l’utilisation métier que l’on veut en faire.

Néanmoins, l’inconvénient de cette méthode, outre qu’elle part d’un modèle supervisé précis qu’on ne voudra peut-être pas utiliser dans certains cas (la forêt d’arbre aléatoires), est qu’elle ne nous permet pas d’utiliser l’ensemble des algorithmes de clustering existants. Notamment, il ne nous est pas possible d’utiliser de méthodes à base de centroïdes, comme le K-Means. En effet, cet algorithme nécessite de pouvoir calculer une distance euclidienne entre chaque point et son centre de masse, or l’algorithme proposé nécessite plutôt d’utiliser une distance de Hamming. De même, il n’est pas possible d’utiliser les méthodes à base de distribution de probabilité, comme le modèle de mélange gaussien.

Ce qu’il faut retenir

• Lors de l’établissement d’un clustering, il est important de bien réfléchir à la manière de calculer la distance entre les points pour que le clustering se base sur les variables qui nous intéressent vraiment ;
• Une manière de faire est de rattacher cette mesure de distance aux résultats d’une modélisation supervisée, si une telle modélisation est faisable dans le contexte ;
• Dans ce cas, l’utilisation de forêt d’arbres aléatoires peut permettre d’obtenir une mesure de distance aux résultats intéressants.

Références

[1] Voir par exemple la notion de coefficiant de silhouette.

Merci à Winson Waisakurnia dont j’ai réutilisé les fonctions d’interprétation de clustering.

Pour aller plus loin, vous pouvez aussi tester les méthodes proposées dans le paquet metric-learn.