Pourquoi la normalisation des données est une étape essentielle lors du traitement de séries temporelles multiples avec des réseaux de neurones

Plus personne n’est surpris de voir à quel point les réseaux de neurones fonctionnent bien sur bon nombre de problématiques (traîtement d’images, de texte, de son) sur lesquels les techniques traditionnelles donnent toujours de piètres résultats. Le défi serait plutôt aujourd’hui de répliquer ces performances sur le traîtement de données tabulaires.

Mais qu’en est-il des séries temporelles ? Si l’on en croit le florilège d’articles vous promettant de pouvoir prédire l’avenir des cours de la bourse, ou le temps qu’il fera dans l’après-midi, on aurait plutôt tendance à les placer dans la catégorie des problèmes pour lesquels les réseaux de neurones ont déjà fait la différence.

Pourtant, les expériences que j’ai pu avoir lors de l’utilisation de LSTM ou de GRU, que cela soit sur des données purement temporelles, ou augmentées de données contextuelles, m’ont montré que la réalité était souvent plus complexe que ce qui est présenté dans les tutoriels. Ceux-ci ont en effet tendance à très peu parler d’un problème essentiel dans de nombreux cas d’applications : la normalisation des données.

Pour pouvoir analyser l’impact de cette technique sur les résultats d’un modèle de prédiction supervisé, nous allons chercher à prédire l’évolution du traffic sur différents articles de l’encyclopédie Wikipedia, modélisation univariée dont les conclusions pourront aisément être étendues à des cas multivariés. Vous pourrez suivre les expérimentations que nous ferons au fur et à mesure grâce au projet github créé à cet effet.

La modélisation d’une série temporelle unique

La première étape de ma modélisation a été de chercher à modéliser l’évolution du traffic sur une page unique, tirée au hasard parmis l’ensemble des pages. Comme vous pouvez le voir dans ce notebook, dans le cas d’une page au traffic relativement faible, les résultats de l’entraînement d’un LSTM sans phase de normalisation sont relativement satisfaisants, considérant le faible nombre de données d’entraînement.

Certains points sont cependant à noter, même s’ils sont bien connus et facile à retrouver :

• en cas de séries multivariées, il aurait été préférable de normaliser les différentes features afin d’une part d’accélérer la convergence de la descente de gradient, et d’autre part d’éviter que certaines features n’aient une influence disproportionnée lors de l’apprentissage

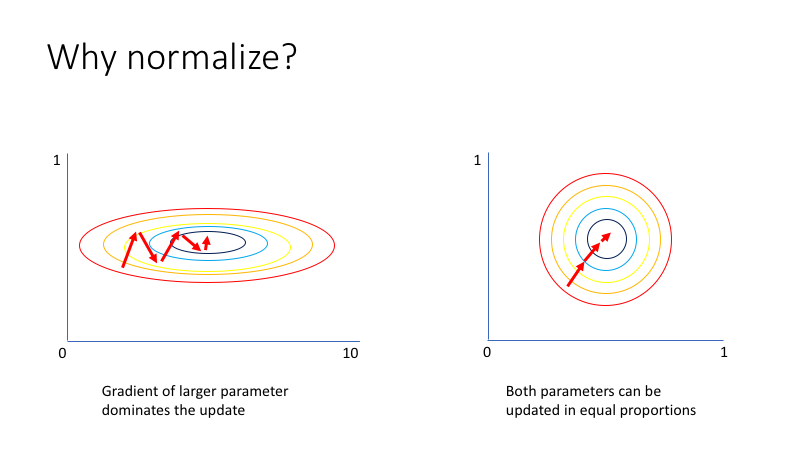
• même dans le cas d’une série univariée, il peut être nécessaire de normaliser la série. En effet, on a généralement tendance à initialiser les poids des réseaux de neurones suivant une loi centrée en zero et d’écart type inférieur à un, et des données trop éloignées en terme d’échelle rendent plus difficile le fait de tomber sur un résultat optimal lors de la descente de gradient (on risque de s’arrêter à un minimum local en cours de chemin). Par exemple, on peut voir dans ce notebook que le modèle entraîné semble faire des prédictions quasi constantes quelle que soit l’entrée. Il est donc préférable de normaliser nos données, afin de ne pas avoir à trop s’éloigner des distributions d’initialisations des poids utilisée habituellement.

Travailler sur plusieurs séries temporelles à la fois

Jusqu’ici, nous nous sommes contentés d’entraîner notre modèle sur une unique série temporelle. Néanmoins, lorsque l’on travaille sur plusieurs séries temporelles à la fois, comme par exemple sur l’évolution du traffic sur l’ensemble des pages de Wikipédia, il peut être intéressant d’utiliser un seul modèle pour l’ensemble de ces séries, plutôt qu’un modèle par série. En effet, cela permet :

• d’éviter d’avoir à entraîner et conserver des centaines voire des milliers de modèles (scalabilité)
• de pouvoir entraîner des modèles sur davantage de données, et ainsi les rendre plus généralisables et améliorer leurs performances

C’est donc ce qui a été tenté dans cet autre notebook, en réappliquant ce que l’on a appris dans la partie précédente. Néanmoins, on se rend compte en regardant les parties 2 et 3 du notebook que cela n’a pas eu l’air de très bien fonctionner. En effet :

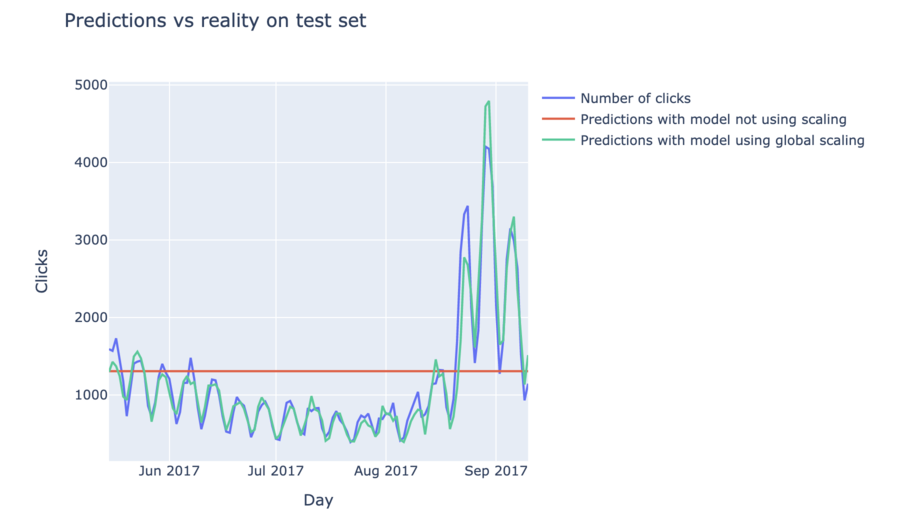
• si on ne normalise pas les données, les résultats sur les petites séries temporelles semblent être corrects, mais le modèle se met à renvoyer des prédictions constantes à partir d’une certaine échelle
• si on normalise les données de manière globale, les résultats ne semblent pas plus satisfaisants. Global signifie ici que, si on pose \(\mu\) la moyenne de l’ensemble des données et \(\sigma\) leur écart-type, on va poser que, pour toute donnée x, \(x^{scaled} = \frac{x - \mu}{sigma}\). On s’aperçoit que les résultats sur les “grosses” séries temporelles sont maintenant bien meilleurs, mais qu’ils sont devenus constants en dessous d’un certain seuil, ce qui au final donne un score encore plus mauvais que sans normalisation.

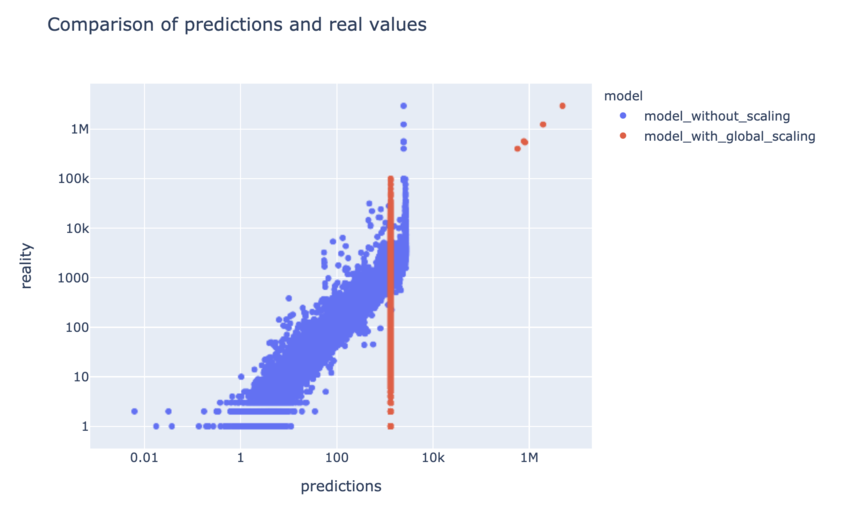
La manière dont on peut interpréter ce problème est que les échantillons utilisés lors de l’entraînement sont trop différents les uns des autres, avec quelques “grosses” séries temporelles qui s’opposent à la plupart des “petites” séries temporelles, chacune s’évertuant de tirer la couverture (ou plutôt le gradient) de son côté. Il semble alors difficile, lors de l’entraînement, de converger vers une solution qui soit à la fois satisfaisante sur les petites séries et sur les grosses.

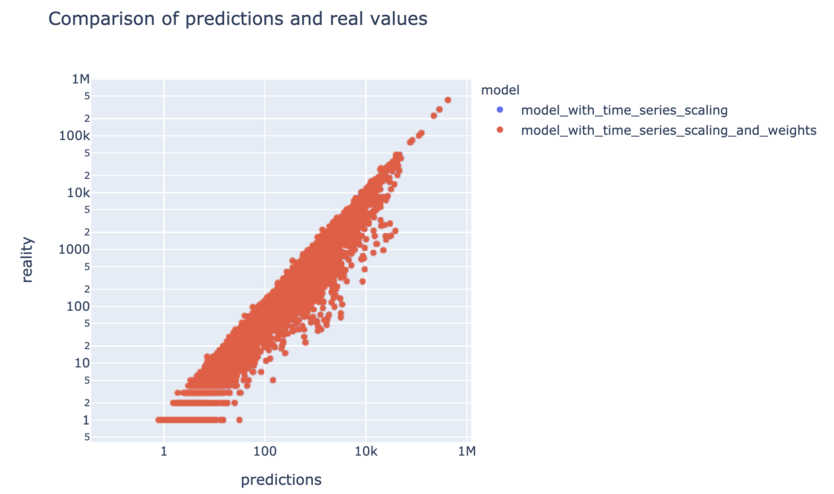
Une solution consisterait à rapprocher ces deux situations qui actuellement s’opposent, en normalisant les données de chacune des séries temporelles de manière séparée. Pour cela, plutôt que de centrer réduire en utilisant la moyenne et l’écart type calculés sur l’ensemble des données, nous allons utiliser une moyenne et un écart type différents par série, correspondant uniquement aux données de la série considérée. Ainsi, pour toute série i et tout instant t, \(x_{it}^{scaled} = \frac{x_{it} - \mu_i}{\sigma_i}\). La suite du notebook nous permet de voir que cet approche offre des résultats très satisfaisants, avec une forte diminution de l’erreur globale et des résultats cohérents à la fois sur les petites et les grosses séries.

La modification de la fonction de coût est-elle problématique ?

En réfléchissant un peu à ce qu’on vient de faire, on se rend compte que le fait de normaliser les données entraîne une modification de la fonction de coût optimisée par le modèle. Celle-ci devient en effet, pour la prédiction d’une variable x à un instant t sur l’ensemble des séries i :

\[L(\hat{x_t}) = \frac{\sum_{i=1}^{N} | \hat{x_{it}}^{scaled} - x_{it}^{scaled} |}{N} = \frac{\sum_{i=1}^{N} | \frac{\hat{x_{it}} - \mu_i}{\sigma_i} - \frac{x_{it} - \mu_i}{\sigma_i} |}{N} = \frac{\sum_{i=1}^{N} | \frac{\hat{x_{it}} - x_{it}}{\sigma_i} |}{N}\]

L’importance de chacun des échantillons d’apprentissage est donc pondérée par l’inverse de son écart-type par rapport à la fonction de coût originelle, qui correspondait juste à l’erreur de prédiction de la variable d’intérêt. Si l’on souhaite revenir à la fonction de coût originelle, une solution est d’utiliser le paramètre sample_weight de keras, en lui affectant pour chaque échantillon son écart-type avant normalisation \(\sigma_{it}\). On aura alors :

\[L(\hat{x_t}) = \frac{\sum_{i=1}^{N} \sigma_{it} * | \hat{x_{it}}^{scaled} - x_{it}^{scaled} |}{N} = \frac{\sum_{i=1}^{N} | \hat{x_{it}} - x_{it} |}{N}\]

Néanmoins, on peut voir dans le notebook que dans notre cas cela n’a pas permis d’améliorer le résultat final. Au contraire, celui-ci s’est très légèrement dégradé. On peut penser que les patterns dynamiques des séries normalisées qui sont ici modélisées sont en fait les même quelle que soit la “taille” de la série ; et que le fait d’avoir des distributions de poids d’échantillons très disparates a plutôt tendance à handicaper le processus de convergence lors de la descente de gradient qu’autre chose. Mais n’hésitez pas à remonter et/ou tester d’autres hypothèses éventuelles !

Que retenir ?

• Lors de la modélisation d’une série temporelle unique, il est préférable de normaliser chacune des variables de ladite série avant d’entraîner le modèle, afin de ne pas favoriser une variable par rapport à une autre, et de favoriser la convergence du modèle
• En cas d’utilisation d’un seul modèle sur plusieurs séries temporelles aux échelles disparates, il est important de mettre toutes les séries à la même échelle, par exemple en les normalisant de manière séparée

Pour aller plus loin

Vous pouvez consulter l’article Impact of Data Normalization on Deep Neural Network for Time Series Forecasting de Samit Bhanja et Abhishek Das, traitant de l’impact de la méthode de normalisation adoptée sur les performances finales

---

---